コンプリート！ 扇形面積 公式 弧度法 305736

2、扇形是与圆形有关的一种重要图形，其面积与圆心角 (顶角)、圆半径相关，圆心角为n°，半径为r的扇形面积为n/360*πr^2。 如果其顶角采用弧度单位，则可简化为1/2×弧长× (半径)。 3、扇形还与三角形有相似之处，上述简化的面积公式亦可看成：1/2×弧长× (半径)，与三角形面积：1/2×底×高相似。 4、弧长 (L)=n/360·2πr=nπr/180，扇形的弧相似三角形的一条边。 参考资料 従って、円の面積公式から、（半径）×（半径）×（円周率）×（中心角）/360 になります。 数式で書くならば、S＝πr^2×A/360 です。 ここで、扇形の弧は、元の円の円周を考えたときの｛（中心角）/360度｝倍になりますから、円の円周の公式から、 2×（半径）×（円周率）×（中心角）/360 になります。三角形の面積（3辺からヘロンの公式） 三角形の面積（1辺と2角から） 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積（4辺の長さから） 台形の1辺・面積（3辺の長さと高さから） ひし形の面積 平行四辺形の面積（底辺と高さから）

高中数学必修四 三角函数突破点 二 弧度制及其应用 每日头条

扇形面積 公式 弧度法

扇形面積 公式 弧度法-（弧度制）循环链条扇形面积计算公式： 扇形面积S=圆心弧度绝对值a×半径r² / 2 圆心弧度绝对值a =扇形面积S×2 /半径r²認識圓面積公式。 22、求算圓面積。 31、認識扇形及圓心角。 32、能計算簡單的扇形面積。 41、能應用圓面積和圓周長公 式，算出複合圖形的面積的 面積和周長。 1數與量 n312 能對非直線的平面 區域，選定適當的 正方形單位，估計 其概略面積，並檢 驗圓

高中数学必修四 三角函数突破点 二 弧度制及其应用 每日头条

扇形面積公式 r*r*π*θ/360 面積：5 2 *314*/360=2916 cm 2 三個大扇形面積：3*2916 cm 2 =8748 cm 2 橢圓形 小扇形角度 兩個三角形(5cm4cm3cm) 角度 3687 。 *2=7374 。 小扇形面積 面積：5 2 *314*7374/360=1608 cm 2 菱形面積 四個三角形(5cm4cm3cm) 面積：4*(4*3*1/2)=24 cm 2 弧形面積公式L=n (圓心角度數)× π (1)× r (半徑)/180 (角度制),L=α (弧度)× r (半徑) (弧度制)。 其中n是圓心角度數,r是半徑,L是圓心角弧長。 扇形r—扇形半徑;a—圓心角度數。 C=2r2πr× (a/360);S=πr2× (a/360)。 弓形 l弧長;b弦長;h矢高;r半徑;α圓心角的度數 。 S首先我們只要弄清楚原來白色的小扇形和整個大扇形的圓心角都一樣是1度（也就是 圓），其他的部分就和上面講過的解法都相同了！ 斜線面積 ＝大扇形－小扇形＝ 斜線周長＝大扇形弧長＋小扇形弧長＋2×（大圓半徑－小圓半徑）

扇形の弧の長さと面積を，弧度法をもちいて表してみよう． 図のように半径が r ,中心角が θ の扇形の弧の長さを l ,面積を S とすると，弧度法の定義より θ = l r だから ∴ l = r θ (1) 面積と中心角の比から S θ = π r 2 2 π ∴ S = 1 2 r 2 θ (2) 以上， (1) ， (2扇形の面積 面積も弧の長さと同様に比例式を使います。 扇形の面積も中心角の大きさに比例するので，半径\(r\)の円の面積は\(\pi r^{2}\)，中心角\(2\pi\)なのでもしくは、単純に、1ラジアンの円弧の長さ（＝半径（r））の θ倍であるため ・扇形の面積は （r 2 θ）/2 扇形の面積の公式：円弧×半径/2 に代入 もしくは、円全体の面積 πr 2 に割合 θ/2π を掛ければ求まる 関連動画一覧 動画タイトル 再生時間 1

おうぎ形の面積 ＝ 円の面積 × 中心角 360° 中 心 角 360 ° ＝ 半径×半径×314 × 中心角 360° 中 心 角 360 ° 重要なのは、 おうぎ形が元の円と比べた時にどれくらいの割合なのか ということ。 たとえば中心角が 270° 270 ° 、 180° 180 ° 、 90° 90 ° 、 45° 45 ° といったおうぎ形は元の円と比べるとそれぞれ 3 4 3 4 、 1 2 1 2 、 1 4 1 4 、 1 8 1 8 の大きさになっているのは明らか(2) 扇形 COD 的面積為 A ∵圓心角 2π（一圈）對應的扇形面積（即整個圓面積）是 πr2 2 故 2 2 A r ⇒ A＝ 1 2 r θ＝ 1 2 r（rθ）＝ 1 2 rs。 例題2 扇形的弧長與面積 已知一扇形的半徑為 18 公分，圓心角為 150°，試求此扇形的弧長及面積。 注意 扇形弧長 s＝rθ，扇形先ほど説明したように，半径1の扇形においては(中心角)=(弧の長さ)なので$\theta$でした． 左の扇形(半径1)と右の扇形(半径$r$)の相似比は$1r$ですから，弧の長さも当然$1r$となります． よって， 半径$r$の扇形の弧の長さは$r\theta$となりますね． 面積の公式

扇形面積公式弧長14 Zilhc

弧度制 弧度与角度的互化的知识点总结 相关视频及试题在线练习 易学啦

8 圓與扇形的面積 81 圓面積 1122 圓與扇形的面積 扇形面積 1122 圓與扇形的面積 解題 1122 圓與扇形的面積 9 規律問題 91 間隔問題 2505 間隔問題 92 找規則 2506 找規則 10 等量公理 101 認識等量公理 2511 認識等量公理 102 加與減的等量 たとえば、半径3cm、中心角が90度の扇形があったとしよう。扇形の公式をつかってやれば、 S = 3×3×π×90/360 = 9π/4 になるんだ。どんな扇形の面積でもバッチコイだね！！ 扇形の面積の公式ってなんでつかえるの？？ 扇形の面積の求め方はあんまり難しくない。About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators

扇形面積8 扇形面積 百度百科 Mqttk

圓的周長與面積 16 扇形弧長計算的練習 Youtube

 重要な公式としては以下の5つです。 円・扇形の公式まとめ 円周： 2πr 2 π r 円の面積： πr2 π r 2 扇形の弧の長さ： 2πr× a 360 2 π r × a 360 扇形の面積： πr2 × a 360 π r 2 × a 360 扇形の面積（弧の長さ l l からの導出）： 1 2lr 1 2 l r ※半径： r r 、円周率： π π 、中心角： a a 、扇形の弧の長さ： l l それぞれについて詳しく見ていきましょう。 2分でわかる！扇形の弧の長さを求める公式 「扇形の弧の長さ」の求め方の基本はわかったね？？ それじゃあ、 扇形の弧の長さの公式 をみていこう！ 扇形の半径をr、中心角をα、円周率をπとすると、 2πr×α/360 で「扇形の弧の長さ」を求められるんだ。19河南中招考试数学卷第14题 解题思路：观察图形可知阴影部分由三角形aod和不规则扇形cdb组成，则 = ，其中 = =2×2 ÷2=2 ，这个用三角形面积公式很容易就能求出来（利用oc oa，直角三角形面积公式），而不规则扇形dbc的面积不能直接求出来，这就需要用到大减小的方法，由图可知 ==π ×

扇形周長題目

扇形面积公式怎么推 生活保健 靓范儿

ひし形の面積 平行四辺形の面積（底辺と高さから） 平行四辺形の面積（2辺と夾角から） 円に内接する四角形の面積（4辺から） 四角形の面積（4辺と対角の和から） 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積PART 5：弧度與扇型面積 (0501) PART 5：弧度與扇形面積 (0501) 假設一個半徑為 的圓，圓面積= ，圓周長= 扇 形 之圓心角為 ，則扇 形 無論弧長或面積佔圓的 定義 (度度量轉換弧度) ，如此定義對三角函數之繪圖，計算都更加方便扇形的弧長與面積公式： 若圓半徑為 r ，扇形 COD 的圓心角 ∠ COD ＝θ（弧度），0 ≤ θ ≤ 2π， 如下圖所示，令扇形的弧長為 s ，面積為 A ，則：

扇形 维基百科 自由的百科全书

無料ダウンロード扇形面積公式 シモネタ

翻轉學習影片描述：講師林雨嫻 講師簡介 林雨嫻老師，目前任教於溪口國小。喜歡與孩子一起學習，熱愛教育。 影片簡介 認識圓面積公式的原理。並且利用公式：圓面積=半徑x半徑x314。扇形面積=圓面積x幾分之幾圓。來解決圓或扇形圖形的複合式面積。影片：例題扇形的面積計算，數學 > 主題式 > 國小 > 空間與形狀 > 平面圖形 > 六年級圓面積與扇形面積。源自於：均一教育平台 願 每個孩子都成為終身學習者，成就自己的未來。扇形の面積扇形ocbは比例関係 2π h =π 扇形OCB （ラディアンを使った場合） 360 h =π 扇形OCB （度を使った場合）

高中数学必修四 三角函数突破点 二 弧度制及其应用 每日头条

圆锥侧面积弧度公式 弧度数怎么求 三人行教育网 Www 3rxing Org

 弧の長さと半径から扇形の面積を求める 実は扇形の場合は、中心角がわからなくとも半径と弧の長さがわかればその面積を求めることができます。 扇形の面積 ＝ 弧の長さ × 半径 ÷ 2扇形还与三角形有相似之处，上述简化的 面积公式 亦可看成：1/2×弧长×半径，与三角形面积：1/2×底×高相似。 扇形面积 公式： S扇=（lR）/2 （l为扇形弧长） = (1/2)θR² (θ为以弧度表示的圆心角) S扇=（n/360）πR² s扇=1/2lr（当知道弧长时） （n为圆心角的度数,R为扇形的半径） 注：π为 圆周率 约等于 一般取314扇形の面積は、 S= r 2 θ/2＝6×6×π/3×1/2＝6π です。 扇形の面積とラジアン、半径、弧の長さの関係 扇形の面積、弧の長さを下記に示します。 扇形の面積 S＝r 2 θ／2 扇形の弧の長さ L=rθ 扇形の面積 S＝Lr／2 扇形の面積、弧の長さ共に、角度（ラジアン）と半径が関係します。

高中数学扇形面积与角的弧度制概念题型 面积最大值时的圆心角弧度数怎么求 哔哩哔哩 つロ干杯 Bilibili

上扇形面積公式弧度 扇形面積公式弧度法 Nyosspixi3bq

6n14 能理解圓面積與圓周長的公式，並計算簡單扇形的面積。 (同6s03) 可由圓周長的實測理解圓周長與直徑成比率，其比率(比值)稱為圓周率，在教學上教師應說明圓周率大約為314。扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角（単位「度」）を表します。 また、2行目の l は扇形の弧の長さを表します。 このページの続きでは、この 公式の導き方 と、 扇形の面積を求める計算問題の解き方 を説明しています扇形の面積 S＝r^2θ/2＝rL/2 上式の通り、扇形の面積は、扇形の弧の長さLに半径rを掛けて2で除した値です。扇形の面積は下記が参考になります。 扇形の面積は？1分でわかる意味、公式、求め方、ラジアンとの関係 扇形の弧の長さとラジアンの関係

扇形面积扇形面积 面积公式 爱华网

扇形面積8 扇形面積 百度百科 Mqttk

 \\\\ 中心角2\pi\,ラジアン(360\Deg)に対する面積は\,\pi r^2\ (円の面積)である \\2zh よって \bm{(中心角)(面積)=\thetaS=2\pi\pi r^2}\ より S=\bunsuu12r^2\theta \\\\ 中学で学習した度数法の場合の以下の公式と比較すると,\ 弧度法がいかに本質的であるかがわかる \bm{扇形とトップ 100 おうぎ形 面積 求め方 円と

扇形弧長題目扇形的弧長 Nulaw

扇形弧長題目扇形的弧長 Nulaw

圆的周长与面积 弧长 扇形的面积 玄数

扇形周长和面积公式 搜狗图片搜索

11弧度制radian 弧长arc Length和扇形面积circular Sector Youtube

1

扇形面積8 扇形面積 百度百科 Mqttk

扇形面积计算圆扇形弧形计算公式谁有计算圆弧长扇形面积和圆锥的面积的公式 尚书坊

初中数学 圆的性质 扇形面积公式及应用 异常重要 每日头条

圆的周长与面积 弧长 扇形的面积 玄数

圓面積公式弧度初中數學 幾何 面積與體積公式 Uuogs

扇形面積弧度中學數學漫談一一扇 Hrkpar

高中数学必修四 三角函数突破点 二 弧度制及其应用 每日头条

扇形面积计算圆扇形弧形计算公式谁有计算圆弧长扇形面积和圆锥的面积的公式 尚书坊

3 9 弧长及扇形的面积 哔哩哔哩 つロ干杯 Bilibili

扇形面積弧度中學數學漫談一一扇 Hrkpar

扇形面積題庫面積和體積 二 Jkveno

扇形的面积公式 哔哩哔哩 つロ干杯 Bilibili

数 你好看 任意角三角函数与诱导公式 知乎

高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月

弧长的公式 早旭阅读网

8年級下數學 弓形面積 特殊等腰三角形面積計算方法 18 4 1 Youtube

扇形面積8 扇形面積 百度百科 Mqttk

题型 2弧长与扇形面积公式的计算 哔哩哔哩 Bilibili

积分求平面图形的面积 玄数

扇形面积怎么求练习题 图片欣赏中心 急不急图文 Jpjww Com

Ppt 弧度制powerpoint Presentation Free Download Id

扇形面积公式 哔哩哔哩 Bilibili

扇形弧长和面积的计算公式 视频在线观看 微短视频网

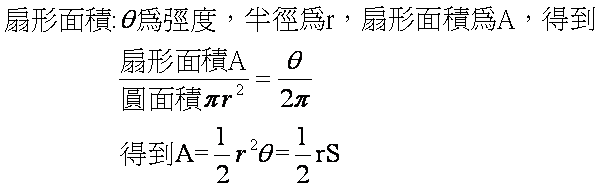
扇形的弧長與面積

上扇形面積公式弧度 扇形面積公式弧度法 Nyosspixi3bq

扇形面積公式弧長14 Zilhc

扇形面积的计算公式 扇形的面积计算公式

扇形面积怎么算 扒拉扒拉

扇形面积公式计算公式 搜狗图片搜索

江苏省常州市西夏墅中学14 15学年高一数学 新人教a版必修四 教案1 1 2 弧度制 下载 Word模板 爱问共享资料

扇形的半径怎么求 扇形的半径怎么算 三人行教育网 Www 3rxing Org

圆弧的弧长怎么计算求计算公式 图片信息欣赏 图客 Tukexw Com

扇形弧长和面积的计算公式 视频在线观看 微短视频网

扇形面積公式 公式 推導過程 注意事項 中文百科全書

圆扇形与弓形

扇形周长和面积公式 搜狗图片搜索

1

扇形面积公式怎么推 生活保健 靓范儿

扇形面積公式弧長14 Zilhc

弧度公式弧度制 360百科 Cxstra

扇形弧長題目扇形的弧長 Nulaw

腾讯视频

扇形面积公式计算公式 搜狗图片搜索

圓的周長與面積 15 如何計算扇形的弧長 Youtube

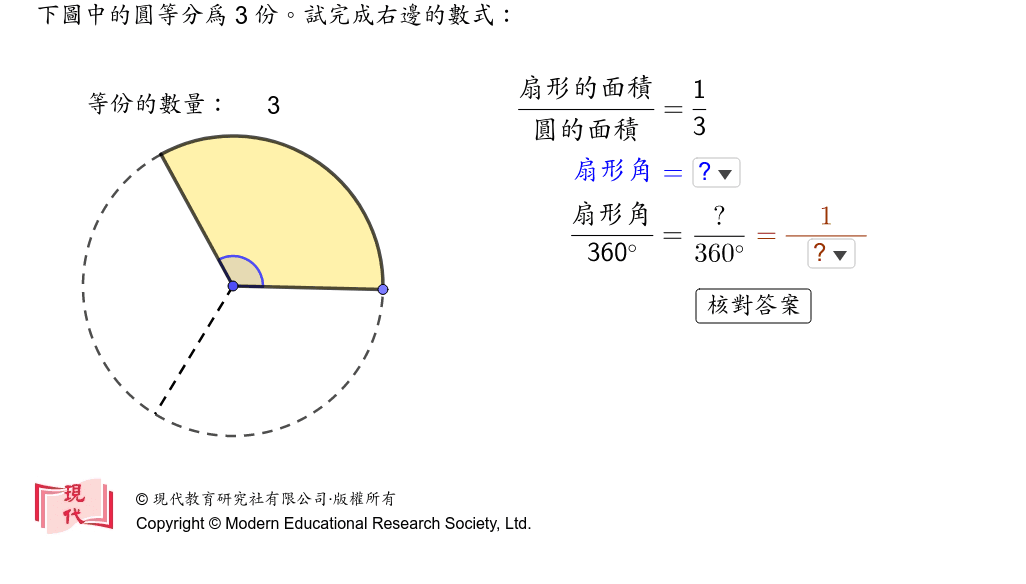
扇形面積公式 Geogebra

扇形面积公式如何推导 Weixin 的博客 Csdn博客

扇形面积公式怎么推 生活保健 靓范儿

圆扇形与弓形

扇形面积公式 弧长公式与扇形面积公式 尚书坊

扇形弧长周长计算方法 视频在线观看 微短视频网

小六扇形面積題目

扇形面积公式 弧长公式与扇形面积公式 尚书坊

高中扇形面积公式是什么 解读扇形面积计算方法 豪友网

2 3 弧度制一 素质教育目标 一 知识教学点1 弧度制的定义 2 用弧度制表示的弧长公式 扇形面积公式 Ppt Download

扇形面积公式带图 万图壁纸网

扇形面积公式带图 万图壁纸网

腾讯视频

扇形面積8 扇形面積 百度百科 Mqttk

扇形面积公式 弧长公式与扇形面积公式 尚书坊

三角函数弧长和扇形面积公式 哔哩哔哩 つロ干杯 Bilibili

扇形面积计算圆扇形弧形计算公式谁有计算圆弧长扇形面积和圆锥的面积的公式 尚书坊

扇形面积公式 弧长公式与扇形面积公式 尚书坊

高中扇形的弧长和面积公式 时尚达人圈

2 圓心角所對弦長 弧長與扇形面積 基本觀念 國三上2 2 Live數學學習網 Www Liveism Com 名師葛倫 Youtube

弧度计算公式 弧度计算公式 弧度 计算 公式 早旭阅读

圆相关公式 Dmp的博客 Csdn博客

腾讯视频

单位圆扇形面积公式 为啥这个单位圆中扇形的面积是2分之一x 三人行教育网 Www 3rxing Org

弧长及扇形面积公式 搜狗搜索

圆扇形与弓形

三角函数弧度制 弧长 扇形面积公式 哔哩哔哩 つロ干杯 Bilibili

扇形的弧長與面積

圆的周长与面积 弧长 扇形的面积 玄数

扇形面積公式弧長14 Zilhc

001 弧度 弧長及扇形面積原理 Youtube

圆弧的弧长怎么计算求计算公式 图片信息欣赏 图客 Tukexw Com

已知弧长求扇形面积公式 搜狗搜索

扇形面积公式怎么推 生活保健 靓范儿

腾讯视频

80 定积分 曲边扇形的面积 哔哩哔哩 Bilibili

高中数学必修四 基础详细讲义附答案38页 小初高题库试卷课件教案网

扇形面積8 扇形面積 百度百科 Mqttk

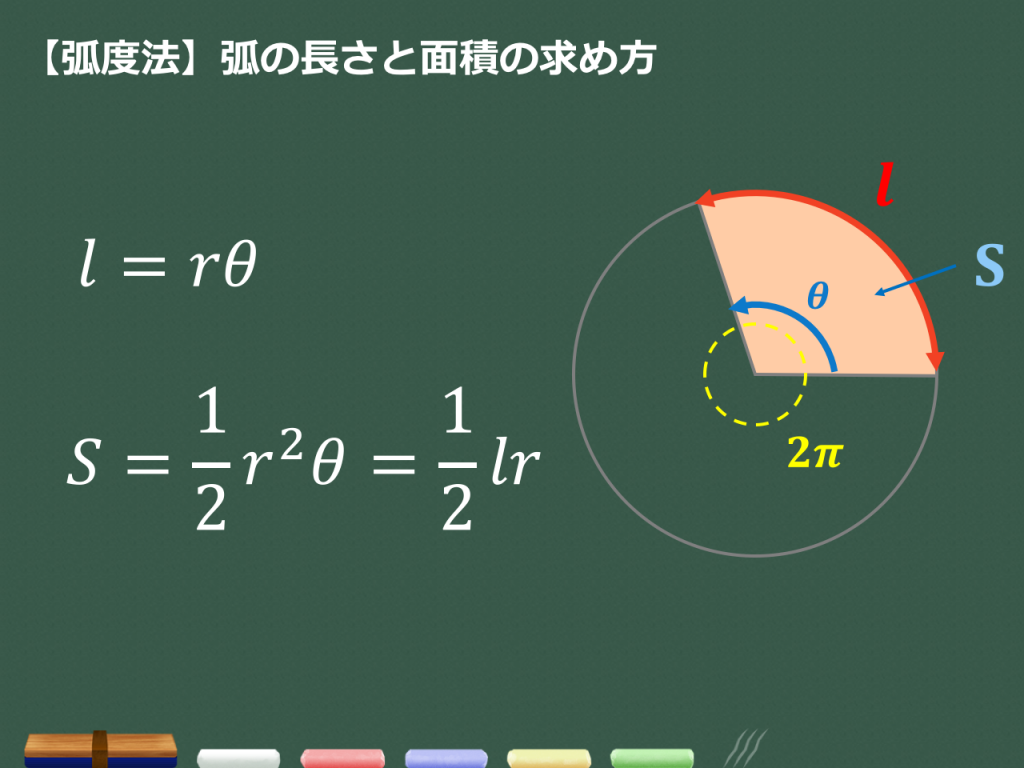
3分でわかる 弧度法 ラジアン の基礎知識 度数法との変換の仕方をわかりやすく 合格サプリ

扇形面積弧度中學數學漫談一一扇 Hrkpar